Free Online Productivity Tools
i2Speak
i2Symbol
i2OCR
iTex2Img
iWeb2Print
iWeb2Shot
i2Type
iPdf2Split
iPdf2Merge
i2Bopomofo
i2Arabic
i2Style
i2Image
i2PDF
iLatex2Rtf
Sci2ools
Presentation
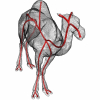
Robust Centerline Extraction Framework Using Level Sets
In this paper, we present a novel framework for computing centerlines for both 2D and 3D shape analysis. The framework works as follows: an object centerline point is selected automatically as the point of global maximum Euclidean distance from the boundary, and is considered a point source (PS) that transmits a wave front that evolves over time and traverses the object domain. The front propagates at each object point with a speed that is proportional to its Euclidean distance from the boundary. The motion of the front is governed by a nonlinear partial differential equation whose solution is computed efficiently using level set methods. Initially, the PS transmits a moderate speed wave to explore the object domain and extract its topological information such as merging and extreme points. Then, it transmits a new front that is much faster at centerline points than non central ones. As a consequence, centerlines intersect the propagating fronts at those points of maximum positive curv...
Real-time TrafficAnimation | Centerline Extraction | Colonoscopy | Computer Graphics | Curve Skeletons | Eikonal Equation | Fast Marching Methods | Gradient Vector Flow | GVF | Medial-axis | Path Planning | Shape Representation | Skeletonization | Virtual Endoscopy |
Related Content
| Added | 09 Nov 2008 |
| Updated | 25 Nov 2008 |
| Authors | M. Sabry Hassouna |
Comments (5)
 | question |
|
|
Submitted by libingdzh on 2008, December 1 - 09:00. |
||
I have a question about the paper."Since centerline points have equal distances from the object’s boundary, then the propagating front at x_i is symmetric around the line segment x_{i-1}x_i and normal to it at page 4. Does every point in the centerline have equal DFB? But they are not same in my opinion. |
||
 | Yes and No |
|
|
Submitted by msabry on 2008, December 1 - 11:14. |
||
Well, theoritically speaking, every point on the centerline have equal distances from the nearest local boundary. However, on the same centerline, points have different DFB depending on the thickness of the object. Do i understand your question? |
||
| DFB |
|
|
Submitted by libingdzh on 2008, December 1 - 19:09. |
||
OK, different points on the same centerline have different DFB depending on the thickness of the object.However, for some point on the centerline, the distance between it and its nearest local boundary is uniform. Do i understand your idea about the first sentence? |
||
| RE: DFB |
|
|
Submitted by msabry on 2008, December 1 - 22:27. |
||
I do not understand what do you mean by uniform. However, let me restate the sentence in a different way. I magine that we have a truncated cone of height H=10, with the largest cross section radius R = 5 and the smallest cross section radius r = 1. Assume that the centerline of the object is aligned with the z-axis. Then the centerline starts at z = 0 with r=1 and ends at z = 10 with R=5. So now, every point z on the centerline have equal distances from the nearest boundary e.x; DFB(z_i) = r_j; where r_j ranges from r=1 to R = 5.
I hope this time it is more clearer than before.
|
||
Researcher Info
|
From Researcher
more...
